Готовьтесь к самостоятельной работе по теме: "Рациональные неравенства"
Справочный материал.
Пусть заданное неравенство имеет вид: 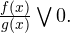 Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Для решения этого неравенства используется так называемый метод интервалов (метод промежутков), который состоит в следующем.
Во-первых, на числовую ось наносят точки  разбивающие ее на промежутки, в которых выражение
разбивающие ее на промежутки, в которых выражение 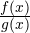 определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений
определено и сохраняет знак («плюс» или «минус»). Такими точками могут быть корни уравнений 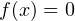 и
и 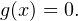 Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Соответствующие этим корням точки отмечают на числовой оси: закрашенными кружками — точки, удовлетворяющие заданному неравенству, а светлыми кружками — не удовлетворяющие ему.
Во-вторых, определяют и отмечают на числовой оси знак выражения 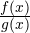 для значении
для значении  , принадлежащих каждому из полученных промежутков. Если функции
, принадлежащих каждому из полученных промежутков. Если функции 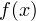 и
и 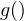 являются многочленами и не содержат множителей вида
являются многочленами и не содержат множителей вида 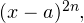 где
где 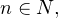 то достаточно определить знак функции
то достаточно определить знак функции 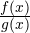 в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
в любом таком промежутке, а в остальных промежутках знаки «плюс» и «минус» будут чередоваться.
Если же в числителе или знаменателе дроби 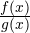 имеется множитель вида
имеется множитель вида 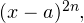 где
где 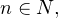 то непосредственной проверкой выясняют, удовлетворяет ли значение
то непосредственной проверкой выясняют, удовлетворяет ли значение 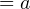 заданному неравенству.
заданному неравенству.
Изменение знаков удобно иллюстрировать с помощью волнообразной кривой (кривой знаков), проведенной через отмеченные точки и лежащей выше или ниже числовой оси в соответствии со знаком дроби 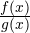 в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие
в рассматриваемом промежутке. Промежутки, которые содержат точки, удовлетворяющие данному неравенству, иногда покрывают штрихами. На ту же ось помещают и точки, соответствующие  Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Заштрихованная область в совокупности с полученными точками будет являться ответом к неравенству.
Примеры решения неравенств методом интервалов
Пример 1. Решите неравенство:
Решение. Упрощаем неравенство путем равносильных преобразований:
При умножении или делении обеих частей неравенства наотрицательное число, меняется знак неравенства!
Выражения, стоящие в числителе и знаменателе, можно разложить на множители, тогда неравенство примет вид:
Далее по алгоритму решения неравенств методом интервалов находим корни уравнений 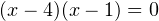 и
и 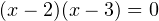 . Из первого получаем
. Из первого получаем 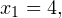
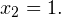 Из второго получаем
Из второго получаем 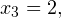
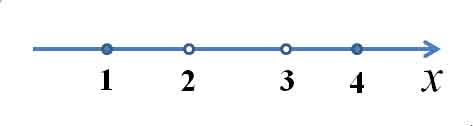
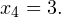 Наносим на числовую прямую получившиеся точки, причем точки
Наносим на числовую прямую получившиеся точки, причем точки 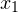 и
и 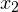 обозначаем закрашенными кружочками (для них неравенство выполняется), а точки
обозначаем закрашенными кружочками (для них неравенство выполняется), а точки 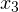 и
и 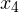 — светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
— светлыми (для них неравенство не выполняется, при этих значениях, выражение, стоящее слева от знака неравенства, вообще не имеет смысла):
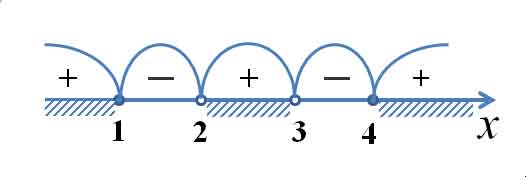
Определяем теперь знаки выражения 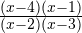 на полученных промежутках (подставляем любое значение
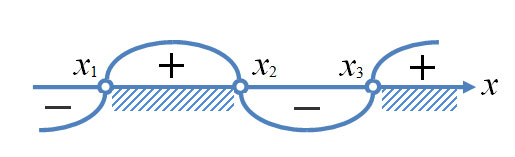
на полученных промежутках (подставляем любое значение 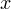 из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
из каждого полученного промежутка в данное выражение), изображаем кривую знаков, заштриховываем те промежутки, на которых исходное неравенство выполняется:
Итак, исходному неравенству удовлетворяют следующие значения: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};1]\cup(2;3)\cup[4;+\mathcal{1}).](http://yourtutor.info/wp-content/ql-cache/quicklatex.com-d46421a915b9249fa4c19ea679359a50_l3.png)
Ответ: ![Rendered by QuickLaTeX.com x\in(-\mathcal{1};1]\cup(2;3)\cup[4;+\mathcal{1}).](http://yourtutor.info/wp-content/ql-cache/quicklatex.com-d46421a915b9249fa4c19ea679359a50_l3.png)


![Rendered by QuickLaTeX.com \[ \frac{1}{x^2-5x+6}-\frac{1}{2}\leqslant 0\Leftrightarrow \frac{2-(x^2-5x+6)}{2(x^2-5x+6)}\leqslant 0\Leftrightarrow \]](http://yourtutor.info/wp-content/ql-cache/quicklatex.com-730734e93796110ee25c6fc4704ef9cd_l3.png)
Комментариев нет:
Отправить комментарий