Иррациональные уравнения и методы их решения

Если в уравнении переменная содержится под знаком квадратного корня, то уравнение называют иррациональным. 

Иногда математическая модель реальной ситуации представляет собой иррациональное уравнение, мы с этим уже встречались. Поэтому нам следует научиться решать хотя бы простейшие иррациональные уравнения. 

Рассмотрим иррациональное уравнение

Это равенство, по определению квадратного корня, означает, что 2х + 1 = З2. Фактически от заданного иррационального уравнения мы перешли к рациональному уравнению 2х + 1 = 9, возведя в квадрат обе части иррационального уравнения. Метод возведения в квадрат обеих частей уравнения — основной метод решения иррациональных уравнений. Впрочем, это понятно: как же иначе освободиться от знака квадратного корня? Из уравнения 2х + 1 = 9 находим х = 4.

Это — и корень уравнения 2х + 1 = 9, и заданного иррационального уравнения. 

Метод возведения в квадрат технически несложен, но иногда приводит к неприятностям. Рассмотрим, например, иррациональное уравнение 

Возведя обе его части в квадрат, получим

Далее имеем: 

2x-4x = -7 +5; -2x = -2; х = 1. 

Но значение х - 1, будучи корнем рационального уравнения 2x - 5 = 4x - 7, не является корнем заданного иррационального уравнения. Почему? Подставив 1 вместо х в заданное иррациональное уравнение, получим  . Как же можно говорить о выполнении числового равенства, если и в левой и в правой его части содержатся выражения, не имеющие смысла? В подобных случаях говорят: х = 1 — посторонний корень для заданного иррационального уравнения. Получается, что заданное иррациональное уравнение не имеет корней.
Решим иррациональное уравнение

-
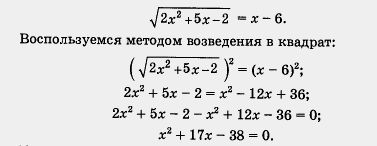
Корни этого уравнения можно найти устно, как мы это делали в конце предыдущего параграфа: их произведение равно - 38, а сумма равна - 17; нетрудно догадаться, что это — числа 2 и - 19. Итак, х₁ = 2, х₂ = - 19. 

Подставив значение 2 вместо х в заданное иррациональное уравнение, получим 

Это неверно. 

Подставив значение - 19 вместо х в заданное иррациональное уравнение, получим 

Это также неверно. 

Каков же вывод? Оба найденные значения — посторонние корни. Иными словами, заданное иррациональное уравнение, как и предыдущее, не имеет корней. 

Посторонний корень — не новое для вас понятие, посторонние корни уже встречались при решении рациональных уравнений, обнаружить их помогает проверка. Для иррациональных уравнений проверка — обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»). Итак, иррациональное уравнение решают методом возведения обеих его частей вквадрат; решив полученное в итоге рациональное уравнение, надо обязательно сделать проверку, отсеяв возможные посторонние корни. Используя этот вывод, рассмотрим несколько примеров. 

Пример 1. Решить уравнение 

Решение. Возведем обе части уравнения (1) в квадрат:

Далее последовательно имеем 5х - 16 = х² - 4х + 4;
х² - 4х + 4 - 5х + 16 = 0;
х² - 9х + 20 = 0;
х₁ = 5, х₂ = 4.
Проверка. Подставив х = 5 в уравнение (1), получим  — верное равенство. Подставив х = 4 в уравнение (1), получим  — верное равенство. Значит, оба найденные значения — корни уравнения (1).

Пример 2. 

Решить уравнение

(это уравнение встретилось нам в § 22 и его решение мы «отложили до лучших времен»)иррационального уравнения, получим 

2x2 + 8* + 16 = (44 - 2х)². 

Далее имеем 

2х² + 8х + 16 = 1936 - 176x + 4x²;
- 2х² + 184x - 1920 = 0;
х² - 92x + 960 = 0;
х₁ = 80, х² = 12.
Проверка. Подставив х = 80 в заданное иррациональное уравнение, получим 

это, очевидно, неверное равенство, поскольку в его правой части содержитсяотрицательное число, а в левой — положительное число. Значит, х = 80 — посторонний корень для данного уравнения. Подставив х = 12 в заданное иррациональное уравнение, получим

т. е. . = 20, — верное равенство. Следовательно, х = 12 — корень данного уравнения.

Ответ: 12. 

 

Разделим обе части последнего уравнения почленно на 2: 

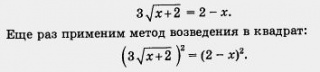
Далее находим:
9 (x + 2) = 4 - 4х + х²;
9х + 18 - 4 + 4х - x² = 0;
- x² + 13x + 14 = 0;
x² - 13x - 14 = 0;
x₁ = 14,  x₂ = -1.

Проверка. Подставив значение x = 14 в уравнение (2), получим  — неверное равенство, значит, x = 14 — посторонний корень.

Подставив значение x = -1 в уравнение (2), получим 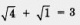 — верное равенство. Поэтому x = - 1 — корень уравнения (2).

О т в е т: - 1.

Пример 4.

Решить уравнение 

Решение. Конечно, можно решить это уравнение по той же схеме, которую мы применяли в предыдущих примерах: переписать уравнение в виде 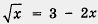 возвести обе части этого уравнения в квадрат, решить полученное рациональное уравнение и проверить найденные корни подстановкой их в
исходное иррациональное уравнение. Но мы применим более изящный способ: введем новую переменную у =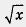  . Тогда получим 2у₂ + у - 3 = 0 — квадратное уравнение относительно переменной у. Найдем его корни: у₁ = 1, у₂ = -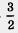. Таким образом, задача свелась к решению двух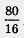 
Из первого уравнения находим х = 1, второе уравнение не имеет корней (вы же помните, что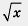  принимает только неотрицательные значения).

Ответ: 1.

Завершим этот параграф достаточно серьезным теоретическим разговором. Дело в следующем. Вы уже накопили некоторый опыт в решении различных уравнений: линейных, квадратных, рациональных, иррациональных. Вы знаете, что при решении уравнений выполняют различные преобразования, например: член уравнения переносят из одной части уравнения в другую с противоположным знаком; обе части уравнения умножают или делят на одно и то же отличное от нуля число; освобождаются от знаменателя, т. е. заменяют уравнение 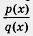= 0 уравнением р (х) = 0; обе части уравнения возводят в квадрат.

Конечно, вы обратили внимание на то, что в результате некоторых преобразований могли появиться посторонние корни, а потому приходилось быть бдительными: проверять все найденные корни. Вот мы и попытаемся сейчас осмыслить все это с теоретической точки зрения.

Определение. Два уравнения f (x) = g (x) и r(x) = s (х) называют равносильными, если они имеют одинаковые корни (или, в частности, если оба уравнения не имеют корней).

Обычно при решении уравнения стараются заменить данное уравнение более простым, но равносильным ему. Такую замену называют равносильным преобразованием уравнения.

Равносильными преобразованиями уравнения являются следующие преобразования:

1. Перенос членов уравнения из одной части уравнения в другую с противоположными знаками.

Например, замена уравнения 2х + 5 = 7х - 8 уравнением 2х - 7х = - 8 - 5 есть равносильное преобразование уравнения. Это значит, что уравнения 2х + 5 = 7х -8    и 2х - 7х = -8 - 5  равносильны.

2. Умножение или деление обеих частей уравнения на одно и то же отличное от нуля число.

Например, замена уравнения 0,5x² - 0,3x = 2 уравнением 5х² - Зх = 20

(обе части уравнения умножили почленно на 10) есть равносильное преобразование уравнения. Неравносильными преобразованиями уравнения являются следующие преобразования: 1. Освобождение от знаменателей, содержащих переменные.
Например, замена уравнения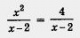  уравнением х² = 4 есть неравносильное преобразование уравнения. Дело в том, что уравнение х² = 4 имеет два корня: 2 и - 2, а заданному уравнению значение х = 2 удовлетворять не может (знаменатель обращается в нуль). В подобных случаях мы говорили так: х = 2 — посторонний корень. 2. Возведение обеих частей уравнения в квадрат.

Примеры приводить не будем, так как их было достаточно много в этом параграфе.

Если в процессе решения уравнения применялось одно из указанных неравносильных преобразований, то все найденные корни надо проверить подстановкой в исходное уравнение, поскольку среди них могут оказаться посторонние корни.

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина,